牛頓一拉森方法

ANSYS程序的方程求解器計算一系列的聯立線性方程來預測工程系統的響應。然而，非線性結構的行為不能直接用這樣一系列的線性方程表示。需要一系列的帶校正的線性近似來求解非線性問題。

逐步遞增載荷和平衡迭代

一種近似的非線性救求解是將載荷分成一系列的載荷增量。可以在幾個載荷步內或者在一個載步的幾個子步內施加載荷增量。在每一個增量的求解完成后，繼續進行下一個載荷增量之前程序調整剛度矩陣以反映結構剛度的非線性變化。遺憾的是，純粹的增量近似不可避免地隨著每一個載荷增量積累誤差，導種結果最終 失去平衡，如圖1所示所示。

                           （a） 純粹增量式解             （b）全牛頓－拉普森迭代求解

                                     圖1    純粹增量近似與牛頓－拉普森近似的關系

ANSYS程序通過使用牛頓－拉普森平衡迭代克服了這種困難，它迫使在每一個載荷增量的末端解達到平衡收斂（在某個容限范圍內）。圖1（b）描述了在單自由度非線性分析中牛頓－拉普森平衡迭代的使用。在每次求解前，NR方法估算出殘差矢量，這個矢量是回復力（對應于單元應力的載荷）和所加載荷的差值。程序然后使用非平衡載荷進行線性求解，且核查收斂性。如果不滿足收斂準則，重新估算非平衡載荷，修改剛度矩陣，獲得新解。持續這種迭代過程直到問題收斂。

ANSYS程序提供了一系列命令來增強問題的收斂性，如自適應下降，線性搜索，自動載荷步，及二分等，可被激活來加強問題的收斂性，如果不能得到收斂，那么程序或者繼續計算下一個載荷前或者終止（依據你的指示）。

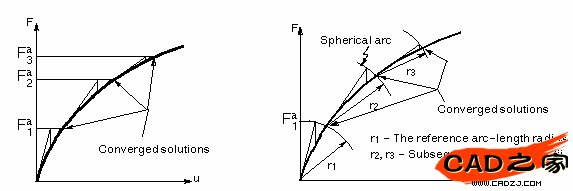
對某些物理意義上不穩定系統的非線性靜態分析，如果你僅僅使用NR方法，正切剛度矩陣可能變為降秩短陣，導致嚴重的收斂問題。這樣的情況包括獨立實體從固定表面分離的靜態接觸分析，結構或者完全崩潰或 者“突然變成”另一個穩定形狀的非線性彎曲問題。對這樣的情況，你可以激活另外一種迭代方法，弧長方法，來幫助穩定求解。弧長方法導致NR平衡迭代沿一段弧收斂，從而即使當正切剛度矩陣的傾斜為零或負值時，也往往阻止發散。這種迭代方法以圖形表示在圖2中。