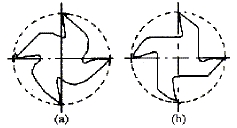
1 引言
2 球頂刃口曲線設計難點及解決方法
- 螺旋刃口的設計難點
- 令球頭銑刀的球面方程為
r={(R2-z2)½cosf,(R2-z2)½ sinf,z} (1)
式中:R———球面半徑- z,f———球面參數
- 球面上與軸線成定角y 的刃口曲線應當滿足微分方程
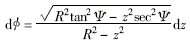 (2)
(2)- 當R2tan2y-z2sec2y<0,即在z> Rsiny 時微分方程無實解,也即在此部分球面上設計不出與軸線成y 角的刃口曲線。
- 后續平面刃口曲線
- 由于在球頭上z∈[Rsiny,R]的部分區域內設計不出與軸線成y 角的刃口曲線,因此只能用其它刃口曲線替代,最簡單的方法是用平面刃口曲線替代。如要保證刃口曲線在連接點處的一階導數連續,且前角相等,取z=Rsiny 的刃口曲線點作為連接點并不合適。由《球頭銑刀刃口曲線的求解及螺旋溝槽的二軸聯動數控加工》可知,磨削溝槽時砂輪的軸向、徑向進給速度分別為
式中:r——溝槽底部所在的截圓半徑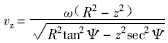 (3)
(3)
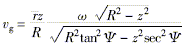 (4)
(4)- w——刀體回轉角速度
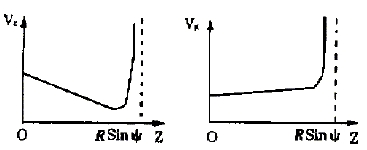
圖1 進給速度曲線
圖2 刃口曲線的截面- 由圖1 所示速度變化曲線可知,當加工接近z=Rsiny 的溝槽時,進給速度v#p#分頁標題#e#z、vg均趨于無窮大,這在實際制造中是無法實現的。因此,在選擇連接點時,應離開z=Rsiny 一定距離,避免因進給速度劇變而給工程實現帶來的困難,選取z=Rsin(y -y0)(y0>0)即可解決這一難題。
- 下面的問題是求平面方程。雖然許多文獻均提及這一問題,但均未給出數學模型,故簡介如下:由《球頭銑刀刃口曲線的求解及螺旋溝槽的二軸聯動數控加工》可求出z=Rsin(y-y0)時得到的刃口點A的坐標( x1,y1,z0)(如圖2所示)以及A點刃口的切線向量為
r1’=( x1’,y1’,z1’) (5)
- 由A 點作Z 軸垂線交Z 軸于B 點,則B 點坐標為(0,0,z0),因此刃口所在平面除過A 點和切向量r1’外,還需過與AB 成g 角的前刀面上的截線AC,由直角三角形ABC 中∠C=p/2,∠BAC=g(前角)可知,C 點坐標( x*,y*,z0)滿足方程組
由上述方程組求出x*和y*,則刃口所在平面方程為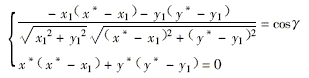 (6)
(6){x1’,y1’,z1’}×{x*-x1,y*-y1,0}×{x-x1,y-y1,z-z0}=0 即z1(’ y1-y*)( x-x1)+z1(’ x*-x1)( y-y1)+[ x1(’ y*-y1)-y1(’ x*-x1)]( z-z0)=0 (7)
- 平面方程(7)與球面方程(1)的交線即為刃口曲線。顯然,這一刃口曲線既與原設計刃口在連接處連續,又對應前刀面有前角g。
- 后續螺旋刃口曲線
- 如許多文獻所述,平面刃口不利于排屑,有文獻提出用橢圓柱與球面交線作為刃口曲線的設想,其目的也是有利于排屑。為使本文不致過于冗長,這里僅對采用另外兩種定義(與經線成定角和等螺距)的刃口曲線替代球頭上z∈[Rsin(y-y0),R]部分刃口曲線的思路作一簡介。
- 事實上,《球頭銑刀刃口曲線的求解及螺旋溝槽的二軸聯動數控加工》已給出了與經線成定角和等螺距兩種刃口曲線的整套計算公式,因此關鍵在于連接點處的計算。這比采用平面刃口法更易處理,只需將點A( x1,y1,z0)的參數f=f( z0)設為求替代刃口曲線在該點相應參數f 時的積分初值即可,這相當于將與經線成定角(或等螺距)的螺旋線連接到已有的與軸線成定角的螺旋線上,由于前角一致,故可按《球頭銑刀刃口曲線的求解及螺旋溝槽的二軸聯動數控加工》的相應方法進行加工,即可得到復合型的兩段螺旋刃口及溝槽。
- 令球頭銑刀的球面方程為
3 球頂刃口曲線的加工問題
4 計算機虛擬制造驗證
5 結語
相關文章
- 2021-09-08BIM技術叢書Revit軟件應用系列Autodesk Revit族詳解 [
- 2021-09-08全國專業技術人員計算機應用能力考試用書 AutoCAD2004
- 2021-09-08EXCEL在工作中的應用 制表、數據處理及宏應用PDF下載
- 2021-08-30從零開始AutoCAD 2014中文版機械制圖基礎培訓教程 [李
- 2021-08-30從零開始AutoCAD 2014中文版建筑制圖基礎培訓教程 [朱
- 2021-08-30電氣CAD實例教程AutoCAD 2010中文版 [左昉 等編著] 20
- 2021-08-30電影風暴2:Maya影像實拍與三維合成攻略PDF下載
- 2021-08-30高等院校藝術設計案例教程中文版AutoCAD 建筑設計案例
- 2021-08-29環境藝術制圖AutoCAD [徐幼光 編著] 2013年PDF下載
- 2021-08-29機械AutoCAD 項目教程 第3版 [繆希偉 主編] 2012年PDF