最近在某論壇上看見一道CAD繪制的趣味練習(xí)題，起初絞盡腦汁不知從何下“鼠標(biāo)”。最后跟著高人學(xué)習(xí)發(fā)現(xiàn)了一個重要的定理，后來發(fā)現(xiàn)該定理對于CAD的使用還是比較有意義的，遂進(jìn)行了詳細(xì)的揣摩理解。在此與大家分享一下阿氏圓定理在中望CAD繪圖中的應(yīng)用。

　　阿氏圓定理(全稱：阿波羅尼斯圓定理)，具體的描述：一動點P到兩定點A、B的距離之比等于定比m：n，則P點的軌跡，是以定比m：n內(nèi)分和外分定線段AB的兩個分點的連線為直徑的圓。該圓稱為阿波羅尼斯圓，簡稱阿氏圓。

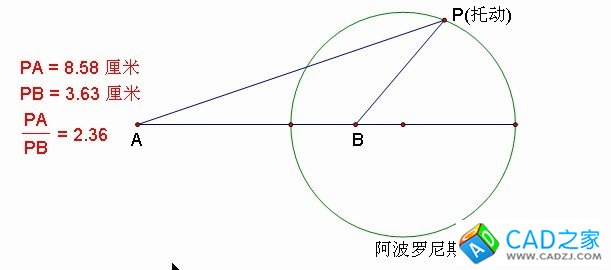
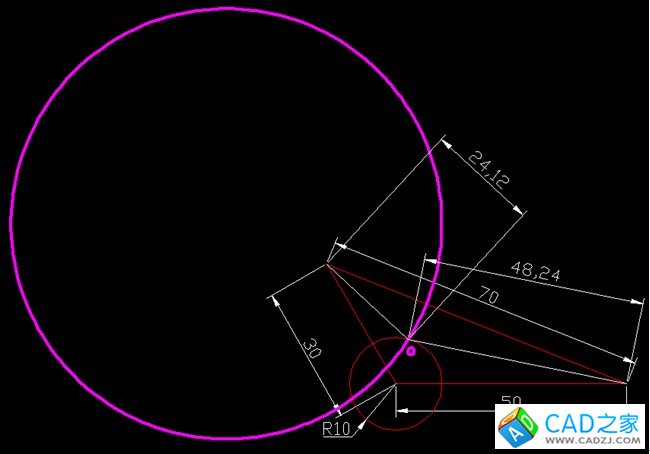
　　舉個例題，各尺寸如下圖所示，求出線段a的長度。

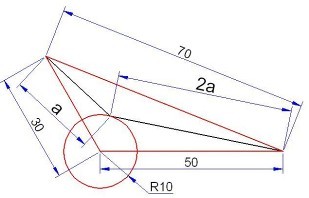
　　分析：其中紅色的線條(即三角形與圓)都非常的容易，那么線段a與2a該如何來求呢。通過上面的定理介紹結(jié)合這兩個線段1:2的關(guān)系。兩線段的交點應(yīng)該是阿氏圓(m：n=1:2)上的一點，并且為與已知半徑為10的圓相交的那一點。

　　首先，我們先將容易的部分作出。然后將70的邊通過divide命令等分為3份(因為比例為1:2)，等分點為A、B兩點。

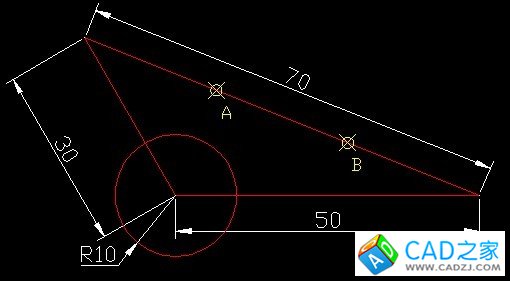
　　其次，以長70的邊的兩個端點為圓心，分別做半徑為R與2R的兩個圓(同樣是為了1:2)，R任意，只要滿足所作的兩個圓相交即可。兩圓交與C、D兩點。

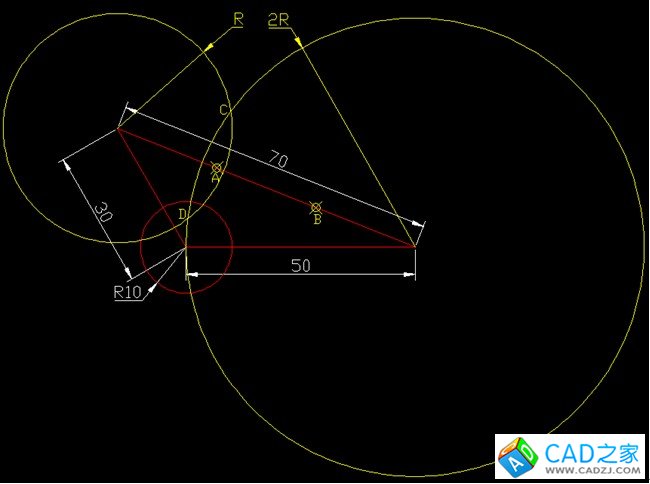
　　過C、A、D點通過三點畫圓，所得粉色的圓即為所求阿氏圓，與半徑為10的已經(jīng)圓交與O點。將黃色的輔助對象刪除，連接O點與長70邊的兩個端點，最后進(jìn)行標(biāo)注即可。

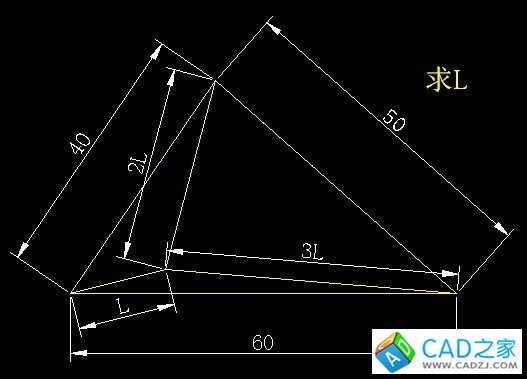
　　到此，a值已經(jīng)求出。不知大家是否已經(jīng)掌握，最后留一個另外一題供大家思考，感興趣的同志可以自己動手嘗試一下。