焊接電流是影響焊絲熔化和焊縫熔深的主要焊接參數，一般在焊接過程控制中常作為恒定的設定參數來考慮。通常焊接電流是由送絲特性曲線與焊接電源外特性交點所決定的，在調節外特性曲線位置而調整電弧電壓時，焊接電流就會隨電壓值的變化而偏離原來的設定值。焊接電路和電弧電壓這兩個主要的規范參數之間的關系是一種非線形的耦合關系，利用人工想很快使焊接電流回復到原設定值是很困難的［１］。另外，由于網絡電壓的波動、保護氣體純度、流量以及焊炬高度的變化等都引起焊接電流的波動。雖然焊機本身具有的自身調節作用，但都會給焊接電流帶來一定的誤差。針對以上情況，本文研制了一種以可編程控制器(ＰＬＣ)為核心器件并自主開發的軟件，實現穩定行ＣＯ２焊焊接電流的模糊控制器。
  模糊控制器具有良好控制效果的關鍵是具有一個完善的控制規則。但對于高階、非線性、大時滯、時變以及隨機干擾嚴重的復雜被控過程，僅靠對操作者實踐經驗的總結或模糊控制信息的歸納，很難設計出適合被控過程不同運行狀態的控制規則。
  為此，本文不采用Ｍａｍｄａｎｉ規則表，而是在基本模糊控制器的設計基礎上，設計了一種帶修正函數自尋優模糊控制器(如圖1)，

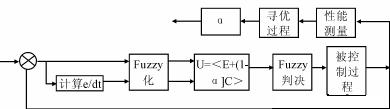
它是一種自組織的模糊控制器［２］；并對所設計的模糊控制器使用ＭＡＴＬＡＢ（含ＳＩＭＵＬＩＮＫ）軟件進行仿真。 

  ２ 模糊控制器的設計 

  ２．１ ei,ei/dt和ui基本論域的確定
  由送絲特性曲線可知，當焊接電流在短路與過渡(小規范)范圍內，電壓每秒變化一伏，電流變化在幾安培之內，當進行中規范焊接時，電弧電壓變化一伏，電流變化最大可達十幾安培。
  本程序把ei在小規范論域設定為［－１０～＋１０Ａ］；ei在中規范論域設定為［－３０～＋３０Ａ］；ei在大規范論域設定為［－６０～＋６０Ａ］。
  在ＰＬＣ系統中ei/dt可以寫為［ｅ（ｋ）－ｅ（ｋ－１）］／Δｔ。Δｔ是指掃描時間，對于某一個確定的程序而言，掃描一次的時間是相同的，因此可以把它設為一個常數，用［ｅ（ｋ）－ｅ（ｋ－１）］的大小近似地代表dei/dt.［e(k)-e(k-1)］的范圍可估計為：０≤｜［ｅ（ｋ）－ｅ（ｋ－１）］｜≤２ｍａｘ［｜ｅ（ｋ）｜－｜ｅ（ｋ－１）｜］，所以可以取dei/dt的基本論域分別為：［－２０Ａ／ｓ＋２０Ａ／ｓ］；［－６０Ａ／ｓ＋６０Ａ／ｓ］；［－１２０Ａ／ｓ＋１２０Ａ／ｓ］。
  為了便于編寫程序，對小、中、大的ei和ei/dt的論域分別給上一個合適的比例因子ｋ１、ｋ２、ｋ３。取：ｋ１＝３ ｋ２＝１ ｋ３＝１／２；得到ei和ei/dt的統一的格式為［－３０，＋３０］，［－６０，＋６０］。
  ei是每次采集得到的u(k)與給定值之差，所以ui的論域可取與ei的相似論域，即為［－３０，＋３０］。
  ２．２ 輸入輸出的語言變量
  在工程實際中，語言變量權ｍ一般取為５～１０檔，結合本系統的具體的性能，本控制器取為５檔。離散的語言變量論域中元素個數ｎ與ｍ的關系為：ｎ＝（１．５－２）ｍ，因此ｎ可取為9，從而ei,ei/dt和ui的語言變量論域E,Ec,U分別為：
  ［－４，－３，－２，－１，０，＋１，＋２，＋３，＋４］
  與此對應偏差量化因子為０．１；偏差變化率量化因子為０．０５；輸出量化因子為０．１。
  ２．３ 模糊控制器的規則
  假設被控對象的實際動態過程可用下式描述：
  Ｙ（Ｋ）＋ａ１Ｙ（Ｋ－１）＋…＋ａｎＹ（Ｋ－ｎ）＝ｂ１Ｕ（Ｋ－ｍ－１）＋…ｂｎＵ（Ｋ－ｍ－ｎ）＋ｅ（Ｋ）＋ｃ１ｅ（Ｋ－１）＋…＋ｃｎｅ（Ｋ－ｎ） （１）
  式中Ｕ（Ｋ），Ｙ（Ｋ）分別為被控對象的輸入和輸出；ｅ（Ｋ）為噪聲干擾率明表示被控對象的傳輸延時；ａｉ，ｂｉ，ｃｉ（ｉ＝１，２，…ｎ）為各項系數。#p#分頁標題#e#
  設計一個預報模型，即根據Ｋ時以前的數據Ｙ（Ｋ），Ｙ（Ｋ－１），…和Ｕ（Ｋ），Ｕ（Ｋ－１），…來預報Ｙ（Ｋ＋ｍ＋１），其中ｍ＝０，１，２，…。根據自適應控制理論，預報模型的方程為：
  Ｙ（Ｋ＋ｍ＋１）＋α１Ｙ（Ｋ）＋…αｐＹ（Ｋ－ｐ－１）＝β０Ｕ（Ｋ）＋β１（Ｋ－１）＋…＋βＵＬ（Ｋ－Ｌ）＋∈（Ｋ＋ｍ＋１） （２）
  式中∈（Ｋ＋ｍ＋１）為預報模型的偏差，令向量ＸＴ（Ｋ）＝［－Ｙ（Ｋ），－Ｙ（Ｋ－１），］…－Ｙ（Ｋ－ｐ＋１），Ｕ（Ｋ－１），…，Ｕ（Ｋ－Ｌ）；
    定義參數向量θＴ＝［α１，α２，…，αｐ，β１，…，βＬ］，則式(2)
可簡化為：Ｙ（Ｋ）＝β０Ｕ（Ｋ－ｍ－１）＋ＸＴ（Ｋ－ｍ－１）θ＋∈（Ｋ） （３）
  對于參數向量θ的估計，可以采用簡單的最小二乘遞推法，其遞推形式為：
  θ（Ｋ＋１）＝θ（Ｋ）＋Ｒ（Ｋ）［Ｙ（Ｋ）－β０Ｕ（Ｋ－ｍ－１）－Ｘ（Ｋ－ｍ－１）θ（Ｋ）］
  Ｒ（Ｋ）＝Ｐ（Ｋ）Ｘ（Ｋ－ｍ－１）［１－Ｘ（Ｋ－ｍ－１—）Ｐ（Ｋ）Ｘ（Ｋ－ｍ－１）］－１?
  Ｐ（Ｋ＋１）＝Ｐ（Ｋ）－Ｐ（Ｋ）［１＋ＸＴ（Ｋ－ｍ－１）Ｐ（Ｋ）Ｘ（Ｋ－ｍ－１）ＲＴ（Ｋ）］ （４）
  式中，θ（Ｋ）和θ（Ｋ＋１）表示在Ｋ和（Ｋ＋１）采樣時刻的參數向量θ的估計量
；Ｐ（Ｋ）是ｍ×ｍ階矩陣，它的維數取決于未知參數的數目，而與測量次數無關。
  因此，可由式(4)求出Ｙ（Ｋ）的預報值，從而求出預測誤差ｅ和誤差的變化率ｅｃ。若給定值為Ｒ，則：
  ｅ＝Ｙ（Ｋ）－Ｒ，ｅｃ＝Ｙ（Ｋ－１）－Ｙ（Ｋ） （５）
  將ｅ和ｅｃ整量化及模糊化后，可得帶有調整因子的規則可調的Ｆｕｚｚｙ控制規則：
  Ｕ＝－［αｅ＋（１－α）ｅｃ］ （６）
  式中，Ｕ為控制量Ｕ的整量值；α為調整因子，又稱加權系數，α∈（０，１）。
  α值的大小，直接反映了對偏差ｅ和偏差變化率Δｅ的加權程度。因此，上式通過調整單一因子的值，就可以很方便地修改控制規則，以改善系統的控制效果。但這種規則的單因子自調整方法存在一些不足，就是其控制規則只依賴一個α參數；一旦確定α，則偏差ｅ和偏差變化率Δｅ的權重就確定了。在實際中控制系統處于不同工作狀態時，要求ｅ和Δｅ的權重不同；當ｅ的絕對值較大時，控制系統的主要矛盾是消除ｅ，故此時應增大α值，使ｅ在控制規則中占較大的權重，以改善系統的動態特性；當ｅ的絕對值較小時，控制系統的主要矛盾是抑制系統超調，使系統盡快達到穩態，故此時應減小α值，而１－α值則相應增大，使Δｅ在控制規則中占較大的權重。用單因子調整控制規則顯然無法實現系統狀態變化的需要。
  為了克服單因子自調整的不足，根據偏差的量化值的大小，提出了一個多因子自調整控制規則的算式：
  采用帶修正因子的控制規則，即使是采用五因子修正算式，α（ｉ＝１－５）值選取仍有較大的盲目性，往往是先憑經驗預定出α的若干個不同的取值，再逐一對它們進行實驗仿真，以選擇最優值。這種方法既耗時又繁瑣，而且往往選不到真正最優的α值。因此還需要設計一種修正因子自尋優的模糊控制器，它能在系統控制過程中對α進行實時自尋優，以實現控制規則的自調整和自完善，達到提高控制系統品質的目的。
  帶修正因子自尋優的模糊控制系統結構如圖1所示，其中通常是取：Ｊ＝∫∞０ｔ｜ｅ｜ｄｔ為目標函數，并以目標函數的值為最小作為系統的性能指標，而且用修正因子α為尋優參數。尋優過程是針對被控過程的運行狀況，根據目標函數值的大小不斷地對因子α進行修正，使目標函數值逐步減小，直到系統的控制性能達到要求為止。若運行狀況發生新的變化，則需重新執行尋優過程，直到調整出適合新運行狀態設為修正因子。#p#分頁標題#e#
  在對給定的輸入響應求目標函數值時，由于用計算機組成的模糊控制系統是一個離散系統，故應把目標函數Ｊ化為離散算式：
  Ｊ＝Σ〖ＤＤ（〗?ｎ〖〗ｉ＝１〖ＤＤ）〗ｉＴ｜ｅ（ｉ）｜Ｔ?＝Σ〖ＤＤ（〗?ｎ〖〗ｉ＝１〖ＤＤ）〗ｉＴ?２｜ｅ（ｉ）｜〖ＪＺ）〗〖ＪＹ〗（８）
  其中：Ｔ是采樣周期，ｉ是采樣序號。
  如果把采樣周期T看成單位時間，則可取Ｔ＝１。式(8)可寫為：
  Ｊ＝Σ〖ＤＤ（〗Ｎ〖〗Ｉ＝１〖ＤＤ）〗ｉ｜ｅ（ｉ）｜〖ＪＺ）〗〖ＪＹ〗（９）
  這樣，只要先憑經驗選擇一組初始修正因子α＝｛α?１，α?２，α?３，α?４，α５｝，得出一組初始的控制規則來對被控對象進行控制，然后對系統響應的過度過程進行采樣，即可用式(9)求出目標函數Ｊ的值。
  在求得系統的目標函數值后，在應用尋優算法進行修正因子α的在線自尋優，使目標函數值Ｊ?＝ｍｉｎ或達到給定值為止。此時的?α??＝｛α?１??，α?２??，α?３?，α?４??，α?５??｝為最優修正因子，系統的特性也達到了最優，其中的尋優算法可采用單純算法(其方法在自動控制理論相關的書籍上都有介紹)。
  ２．４ 模糊控制表的完成
  當選用不同的修正因子時，根據公式(7)就會得到不同的模糊控制規則而形成不同的模糊控制表。對于弧焊電源這樣一個典型的被控對象，其傳遞函數假定為：Ｇ（ｓ）＝１／ｓ（ｓ＋１）。設給定的輸入為單位階躍輸入信號，現采用修正因子自尋優方法對以上對象進行控制。為了得到最優的α值，首先憑經驗預定出5個不同的取值α?１＝０．３，α?２＝０．４，α?３＝０．５，α?４＝０．６和α?５＝０．７；再以式(9)表示的J為尋優目標，采用單純形法作為尋優方法，經過多次調整最終找到Ｊ＝ｍｉｎ的最優修正因子為：?α?１??＝０．２８，α?２??＝０．５０，α?３??＝０．６６，α?４??＝０．７９，α?５??＝０．９３。?
  ２．５ 模糊控制輸出量的反模糊化
  將上面得到的控制量的論域乘以比例因子，便可得到實際的控制增量，加上原來的控制量，輸出去控制被控對象。若在(4)的基礎上，不對輸入輸出量進行量化，而對所得到的一組優化修正因子進行曲線擬合，得到修正因子的連續表達式，則可獲得連續的輸出量。對修正因子進行擬合運算的模糊控制系統見圖1。這樣可消除量化誤差和調節死區。
  綜上所述，帶修正因子的自組織模糊控制器可以拋開控制表，把模糊控制規則綜合成一個簡單算式，直接求取控制量，并可以根據系統的運行狀態，通過調整α值，很方便地進行在線調整控制規則，以改善系統的控制性能。因此這是一種既方便又有效的自組織模糊控制器，特別適合于工程上應用。 

  ３ 模糊控制器的仿真和分析

  由于模糊控制器的設計思想是模擬人腦的思考過程，在模糊控制器的設計過程中，對實際經驗的依賴性很大，要求設計者結合實際經驗，選取控制量，設計控制規則。選取的某些控制量和控制規則的效果如何，必須編制大量的程序進行仿真分析，或者是等到控制器完成以后通過實際來觀察、驗證。顯然，這兩種方法都費時費力，而且都必須通過大量實驗才能確定，實際設計過程中，類似的工作往往占總工作量的大部分。針對上面的情況，本文使用ＭＡＴＬＡＢ(含ＳＩＭＵＬＩＮＫ)軟件進行仿真。
  ３．１ ＳＩＭＵＬＩＮＫ中的模型的創建方法
  一般模型元件的創建，關鍵在S函數的正確編制及調用。S函數實質上是具有特殊調用格式的ＭＡＴＬＡＢ函數，表征系統動態特性，能使ＳＩＭＵＬＩＮＫ有能力構造一般的仿真方框圖，靈活方便的設計出用戶的特殊環節。
  實際上，ＳＩＭＵＬＩＮＫ的每一個模型都可以用輸入、輸出、狀態三個要素進行描述：
  ｆｕｎｃｔｉｏｎ［ｓｙｓ，ｘ０］＝ｓｆｕｎｃ（ｔ，ｘ，ｕ，ｆｌａｇ，參數1，參數2，…）??［３］?#p#分頁標題#e#
  其中，ｓｆｕｎｃ是用戶定義的系統，ｔ是當前時刻，ｘ是當前狀態值，ｘ０是初始狀態值，ｕ是當前系統輸出值，變量ｆｌａｇ的值返回變量ｓｙｓ的信息。
  模糊控制原理如圖1所示。其中具有調整因子的模糊控制環節，用S函數描述如下：
  zt fuzzy.m
  function［sys,x0］=zt fuzzy(t,x,u,flag,ke,kc,ku,a)
  if abs(flag)=3
  E=round(ke*u(1));
  C=round(ke*u(2));
  Sys=ku*(a*E (1-a)*c);
  Else if flag=0
  Sys=［0;0;1;2;0;0］;
  Elae
  Sys=［］；
  End
  將上述S函數進行成組(Group)和封裝(Mask)處理，就得到用戶創建的ＳＩＭＵＬＩＮＫ模塊。在系統仿真中新模塊與ＳＩＭＵＬＩＮＫ提供的標準模塊功能完全一樣，具有相同的仿真效率及可信度。
  ３．２ 模糊控制器的仿真及分析
  將上述S函數經過封裝處理后，在ＳＩＭＵＬＩＮＫ模型庫中找出與設計的系統相對應的模塊，把它們拖到新模型窗口中，用線連接起來就可以創建一個如圖2示的模糊系統模型圖。

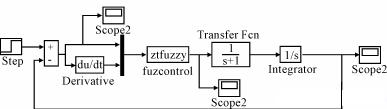
  利用該模型就可以對所設計模糊控制系統進行仿真研究。圖中ＺＴＦＵＺＺＹ模塊是自建的
  模糊調節器模型，圖中step是仿真時輸入的階躍信號，焊接電流的傳遞函數假設為：?Ｇ（ｓ）＝１／ｓ?（ｓ＋１）?，圖中的示波器ｓｃｏｐｅ的作用是實時的畫出控制系統的輸出結果曲線，也可以將數據存儲到ＭＡＴＬＡＢ的工作空間中，再利用繪圖ｐｌｏｔ命令將輸出曲線在單獨窗口畫出來。
  采用多修正因子的自調整規則進行控制仿真的結果如圖3所示。其中曲線3對應于五個修正因子α?１＝０．３，α?２＝０．４，α?３＝０．５，α?４＝０．６和α?５＝０．７時控制系統的單位階躍相應，曲線2應于五修正因子α?１??＝０．２８，α?２??＝０．５０，α?３??＝０．６６，α?４??＝０．７９，α?５??＝?０．９３?時控制系統的單位階躍相應，而曲線1是系統在線調整修正因子時控制系統的相應曲線。由圖可見，離線優化的因子(曲線2)的控制較未優化(曲線3)的控制效果要好，而在線調整因子(曲線1)控制效果最好，超調最小，相應時間最短。但由于在線優化給控制器增加了負擔，使實時效果降低。

  ４ 結論

  1)所設計的穩定ＣＯ?２焊焊接電流模糊控制器不僅可以有效的消除電弧電壓調節過程中所引起的焊接電流的偏差，而且也可以消除網絡電壓波動、保護氣體純度或流量以及焊炬高度變化所引起的偏差。
  2)設計焊接電流的帶修正函數自尋優模糊控制器的穩定性好，階躍響應的超調小，動態響應快。